Nileopt

NILEOPT is the third addition to the VINEOPT family. It is a program for visualization and optimization of nonlinear functions.

It can use OpenOpt for optimization of problems of any dimension and with constraints.

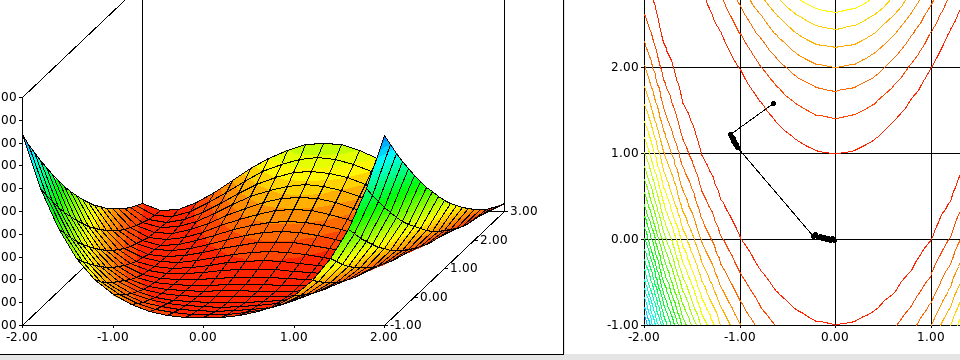
Its main use, however, is for nonlinear problems in two variables, without constraints. Then it draws a 3D-surface of the function and a contour graph. One can then use various search methods, one iteration at a time, and get each iteration point draw in the contour graph.

The problem is entered in a simplified version of the modeling language AMPL/GMPL, that only allows explicit polynomials, not sums over sets, no paratheses, no trigonometric functions. Such a problem can be saved and easily edited. Explicit gradients and Hessians can be calculated.

There is also a prepared set of functions of more general type, including many of the classical testfunctions, such as Rosenbrock, Himmelblau, Zettl, Greiwank and the three/six hump camel backs. These functions can not be edited.

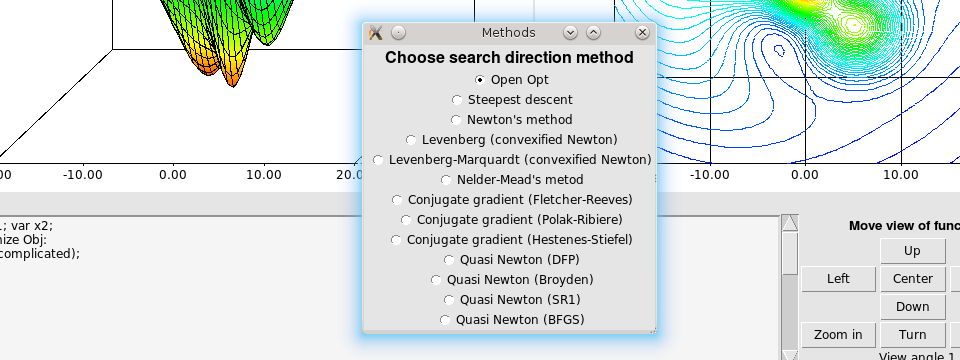
Optimization methods

NILEOPT contains implementations of the following optimization methods. (The implementations are in Tcl, so it rather slow, but that doesn't matter if the main purpose is to see each iteration point.)

• Steepest descent.
• Newton's method.
• Levenberg (convexified Newton).
• Levenberg-Marquardt (convexified Newton).
• Nelder-Mead's metod.
• Conjugate gradient (Fletcher-Reeves).
• Conjugate gradient (Polak-Ribiere).
• Conjugate gradient (Hestenes-Stiefel).
• Quasi Newton (DFP).
• Quasi Newton (Broyden).
• Quasi Newton (SR1).
• Quasi Newton (BFGS).

It can calculate numerical approximations of gradients, but not of Hessians, so all methods that use gradients and not Hessians can be used for all problems. Those that require Hessians can only be used on the simpler type of functions.

Line search can be done accurately or sloppy, or with step equal to one.

Now a preliminary (sligthly simplified) Windows version is available for download here.